2D狂想

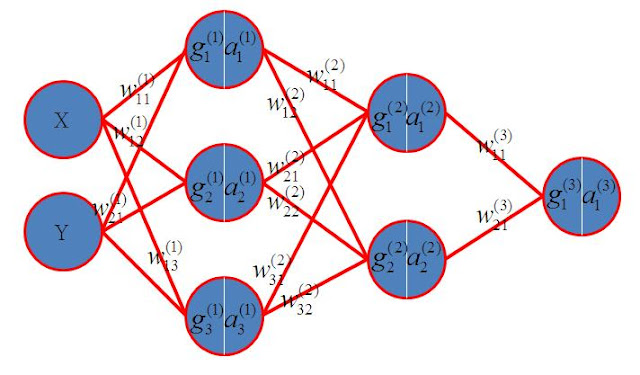
倒傳遞法是一個很舊的東西，但講的類神經網路訓練，就非得提到他。我們也來理解倒傳遞原理。 如上圖，是一個兩個隱藏層的網路。我們的標示法是字母右上角代表第幾層。字母右下角是連線的索引。每個神經原包含 g 跟 a。a是g經過activation function的結果。 如果activation function是sigmoid表示如下， 因為不同網路會選擇不同的activation function因問題與網路會有所不同，我們都以 來表示。 最右邊的神經元是輸出神經原。w為連線的權重。到這裡，我們可以了解當我們在這個網路上輸入X與Y，就會得到一個輸出， 每一次輸出，我們都會想要得到一個差異值，這個差異值代表輸出離我們的目標有多遠。假設我們的目標值為A。那差異就是 我們取平方值可以不用理會差異的正負，1/2是為了微分時方便。有人說不要1/2可以嗎？當然也可以，只是之後推導不方便。我們總要輕鬆的去想一些事情，常數項只要不影響結果，可以想辨法拿掉就拿掉，這是一個技巧。 我們訓練網路，無非就是想要得到各連線的w，用數值的方法，我們可以每次只變化一個權重，觀察輸出往大或小移動。就可以了解這個權重如何影響輸出。把每個權重對輸出的影響都畫成圖，就可以找到讓輸出最接近理想值的權重了。但這樣其實很耗時間。這是今天為什麼需要演算法的原因之一。我們可以寫一個沒有效率的廻圈來算1加到100，也可以像高斯觀察到把數列反序寫，跟原本數列一個一個相加，全都是101，近而產生梯形公式。當然，只要運算能力夠強大，就都不是問題。偏偏人們思考的問題，以目前的科技，運算能力總是不夠強大。 所以我們想了解每一個連線權重對Err的影響，就要用微分。如果我們想知道第二個隱藏層第一個神經原的第一條連線與Err的關係如下  如果我們想知道輸入x的神經原的第一條連線與Err的關係如下 微分也就是斜率，斜率為正，就代表權重變大，會讓Err變大。斜率為負，就代表權重變大Err會變小。所以只要知道每一條連線相對Err的微分，就可以有效率的調整權重的方向了。這樣是不是比數值方法快許多！ 接下來我們推導一下 使用 Chain Rule 這樣

引用一下朋友 怎 的文章 https://losealittle.blogspot.tw/2017/08/blog-post.html 全文貼上。 https://quickdraw.withgoogle.com/ 這個google的網頁，實驗AI辨識人手畫的圖案。非常神的是只要畫沒幾筆就可以被AI猜出來。這已經比人腦還要強。驚訝之餘，我們好奇，是不是AI已經看到了人們眼中的世界。但是，人是這樣的生物，都是用自我在看這個世界，所以你的世界，我的世界不會長一樣，但在講"世界"這兩個字時卻可以概念上一樣。AI真得能理解？ 夫子：所以在哲學上我們會認為這是一種認知的普遍性，也就是你和我在講茶杯，大家都會認知茶杯是一個可以裝水的容器，但你叫大家把茶杯畫出來，全都不會長一樣。所以普遍性是人腦思考的一個對象。 二三子： 嗯嗯？對象？ 夫子：但認知上都不一樣的東西，我們卻可以溝通。為什麼？就是認知的普遍性，有這個普遍性，我們才能討論跟溝通，才能分辨對錯。也才能產生科學。 二三子：哦!?那普遍性的反面是什麼？ 夫子：個別性。你看看你們手上的紙啊！為什麼子一你的杯子有柄，而子二的沒有？為什麼子二的杯子是寬口，而子三的杯子是高腳杯？這就個別性。或者說是特殊性。 了解這個差異我們會發現，人工智能是什麼，人工智能就是科學，科學就是普遍性。 二三子：我懂了，所以說，人類智能是個別性，每個人不同。所以人腦就不科學，不科學所以我們稱其為哲學。 夫子：啊~~~~上次只有子夏讓我有這樣的感覺啊…二三子… 二三子：所以說，有時候我們發現人為什麼講不聽，為什麼懶，為什麼排斥學習。那是因為這個人腦偏向了人工智能。也就是說如果人學的東西，偏向普偏性，這個人就會變的固執，也就越不是人。 夫子：二三子，你們太讓我驚奇了，舉個例子讓我聽聽。 二三子：如果你讓人工智學習認杯子，叫很多人畫杯子，讓人工智能學杯子這個概念。最後你會發現，只要你畫出一個U字形，他就會猜得出來，這就是杯子的普偏性概念。但明明很多人畫杯子會加上手柄，上面會有開口，這些都不重要，因為人工智能學的是所有人畫的普偏性概念。對於特殊性的東西，他就會忽略了，這也是人工智能沒有靈魂的原因，因為他沒法學特殊性。反過來思考，我們可以認定，如果一樣人只學普遍性概念，是不是就會變